More reasons why cheaper devices tend to lose you money instead of making it:It may be tempting to purchase a cheaper device, but the very reason they are cheaper in the first place is because they tend to lose money, or can only be applied successfully on very few wheels. Below are some of the reasons for this, and the problems with roulette prediction that need to be overcome.
Problem 1: HOW the ball will fall Especially on modern wheels, the ball does not hit a vertical diamond, then be deflected predictably down on nearly every spin. This may have been the case with wheels 10 years ago, but it isn't anymore. On modern wheels, even if a computer correctly predicts where the ball will lose momentum and fall, predictions will not be accurate. Why not? Because the ball may hit a horizontal diamond and be deflected to the other side of the wheel. The ball may clip a horizontal diamond, then hit a vertical diamond. The ball may hit a vertical diamond solidly. It may even completely miss all diamonds. Whatever the case may be, the different types of ball falls often have completely different outcomes. Putting this into perspective, for a computer to beat modern wheels, it must know not only where the ball will fall, but also HOW it will fall. Our computer is the only computer available anywhere that determines not only which diamond will be hit, but which part of the diamond will be hit, and the resulting manner in which the ball falls.
Problem 2: WHERE the ball will fall For now, forget about HOW the ball will fall and consider the following: to know WHERE the ball will actually fall from the ball track, the computer MUST account for the fact that wheels are NEVER perfect. In fact ball tracks have many imperfections that appear subtle, but they actually have an enormous influence on where the ball will actually fall from the ball track. Every roulette computer except ours assumes the ball will either:
Does the ball actually fall simply when it reaches a certain speed? NO. There are numerous factors that determine where the ball is going to fall, and when. See below the three types of wheels you will encounter:
Problem 3: Air pressure and ball deceleration rate variations In any environment, air pressure gradually varies over time. When air pressure varies, the deceleration rate of the ball, AND the speed at which the fall falls from the ball track also varies. This means the overall distance the ball will roll will also vary. A player can no more change air pressure than they can change the weather. Significant air pressure variations often occur within approximately 30 minutes, but the change occurs gradually. Consider the following example: if the ball was released at a particular speed, the ball may complete 18 revolutions before falling. Now if the ball is released at the exact same speed just one hour later, even a very slight air pressure variation may mean the ball will complete 21.3 revolutions before falling - that's a difference of 3.3 whole revolutions, and about 4 extra seconds before the ball falls. Here's how this will affect affect accuracy if the computer does NOT account for the air pressure variations:
For a computer to make adjustments for air pressure variation, it MUST use polynomials. Polynomials are mathematical equations used to generate a "best fit" curve to model the deceleration of the ball.
LEFT: The blue dots represent the actual ball timings. the red line is the "best fit" polynomial curve. The polynomial curve can be seen on our computers in the settings. You can see that despite the obvious timing errors (blue dots) the polynomial curve is smooth and accurate.
As air pressure naturally varies in the casino environment, the ball's deceleration rate will naturally change too. Even a very slight change in ball deceleration rate may make the ball travel several additional revolutions. See the chart below for explanation:
The yellow area shows the additional difference traveled. Within only 30 spins in the casino (about an hour), this difference in distance is often over 3 revolutions. In the case of roulette computers, we only consider the last 7 or so seconds before the ball falls, not the whole spin, but the effects are still more than significant. Even solely the difference in speed at which the ball falls can make the ball travel an extra revolution. Especially on modern wheels where there is very little margin for error when predicting which diamond will be hit, and which part of the diamond will be hit, even an error of 1cm may result in a computer producing near random results. Modern roulette wheels are designed to ensure this.
IMPORTANT: Some roulette computer vendors may argue that air pressure variations are not significant. This is because they don't own their own wheels, and they develop their devices on DVDs of roulette spins where a spin occurs every 20 seconds. In such cases, air pressure will not vary much for even 50 spins - after all, it is only about 20 minutes of footage. But in real casino conditions, 50 spins is closer to 2 hours of play, and in that time, air pressure variations can dramatically affect where the ball lands.
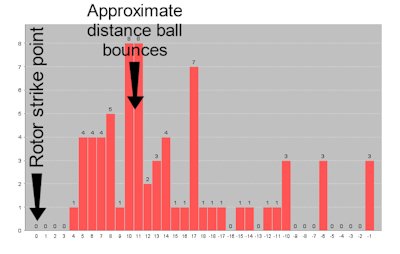
Problem 4: Varying ball bounce and scatter with different wheel speeds When the wheel spins at different speeds, the ball of course behaves differently. This should be obvious to anyone. In fact, even an imperceivable difference in wheel speed may mean the ball bounces to the opposite side of the predicted area on the wheel. For now let's forget all of the other problems with roulette prediction, and assume a computer perfectly predicts where the ball falls, and how it falls. So let's assume the computer knows exactly which pocket the ball will first hit when it falls. Of course the ball will bounce off the initial pocket before coming to rest elsewhere, but for now we're just talking about where the ball first hits on the rotor (called the "rotor strike point"). With the exception of our computer, every computer assumes the ball will bounce the same distance from the rotor strike point irrespective of the wheel rotor speed. So let's say we charted the distance between the rotor strike point to where the ball actually landed, we would expect the chart to look like below:
LEFT: This is called a ball scatter chart. On the horizontal axis, the value of "0" is where the ball actually hits the wheel rotor (the part with the pockets). You can see the ball bounces and comes to rest approximately 10 pockets from the rotor strike point. Most roulette computers conduct analysis based on the assumption that the wheel rotor speed is exactly the same every time. This incorrect assumption alone often makes some roulette computers completely ineffective.
So while a typical scatter chart initially sounds good in theory, the reality is when the wheel is at different speeds, the ball may behave completely differently. Especially on modern wheels, even the slightest difference in wheel speed can mean the ball bounces an extra 12 or more pockets - modern are designed this way. In such cases, if the computer assumes the wheel is spinning at the same speed every time, accuracy may be no better than random. Unlike competing computers, our computers adjust predictions based on the wheel speed of individual spins, and they do this AUTOMATICALLY.
You get what you pay for: Our roulette computers are the only devices that correctly address ALL of the above problems. The competing computers fail to address even one of them, even though just ONE of the problems may make an ordinary roulette computer completely ineffective on modern wheels. So it should be no surprise that they produce virtually random results on modern wheels. Indeed you get what you pay for. Other device sellers choose to ignore the above issues, either because they lack the required expertise, or because they choose to hide the inadequacies of their devices. We do not develop our technology as a hobby, or with the primary purpose of selling it - we develop our technology primarily to use it ourselves, and it is a multi-million dollar business for us. We have invested considerable resources to ensure our technology is literally as good as it can be. Our computers are not cheap, but considering they can return the investment within hours when other computers tend to lose you money, the choice should be clear. With the exception of our micro controller version, all of our computers predict:
Beware of microprocessor (microchip) computers: Virtually anyone with a basic knowledge of programming and electronics can assemble a microprocessor roulette computer, create a website for it, then call it is the best computer money can buy. Microprocessors are like programmable stopwatches. They have very basic functionality. Years ago when roulette wheels were much easier to beat, microprocessors were a popular choice for roulette computers. This is because the microchip itself costs about $5, and you can write a program for them in a matter of hours. In fact some of the roulette computers we've developed ourselves use programmable microprocessors. We sell one of these versions of ours for US$1,850. It includes the wireless transmitter and receiver for 2 players. However, it does not come with the 200% money-back guarantee that it will beat modern designs. This is because programmable microprocessors are extremely limited hardware. They are fine for beating older and heavily tilted wheels, but NOT modern wheels - even on the easily beaten wheels, they do NOT do the job fully. Microprocessor roulette computers are incapable of beating modern wheels primarily because:
For these reasons, long ago we abandoned
development of our roulette computers on microchips. We can still
provide microchip computers upon request, although they are not subject
to the performance guarantee. |

 Hardware is suitable for required functionality, although PDAs are far too large.
Hardware is suitable for required functionality, although PDAs are far too large.  his phone version for free by an unhappy purchaser who believes the
computer is a scam (photo shown left). I can only describe this device
as the clumsiest roulette computer I've ever seen - it is actually worse
than his previous computer and I can confidently say it indeed is a
scam. The original purchaser who sent it to us for free believed the
same, but Howe refused to give a refund. There is no chance it earned
Howe almost US$8M as he claimed - Howe is well known for his outrageous
false claims, both about his competitors and his own products.
his phone version for free by an unhappy purchaser who believes the
computer is a scam (photo shown left). I can only describe this device
as the clumsiest roulette computer I've ever seen - it is actually worse
than his previous computer and I can confidently say it indeed is a
scam. The original purchaser who sent it to us for free believed the
same, but Howe refused to give a refund. There is no chance it earned
Howe almost US$8M as he claimed - Howe is well known for his outrageous
false claims, both about his competitors and his own products.
 very basic functionality. In some respects, it is similar to our PIC
models. This hardware cannot support a design that is sufficiently
sophisticated to beat modern roulette wheels.
very basic functionality. In some respects, it is similar to our PIC
models. This hardware cannot support a design that is sufficiently
sophisticated to beat modern roulette wheels.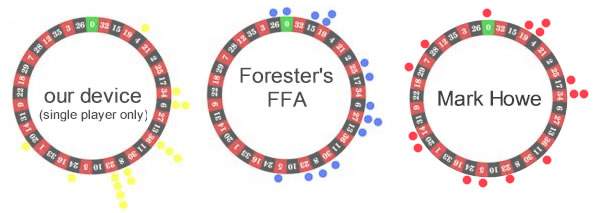
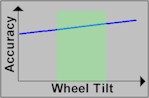
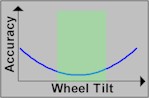
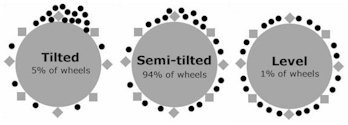 LEFT: The black dots represent where the ball loses momentum and falls from
the ball track for each type of wheel (this is just where the ball loses
momentum and falls, NOT where it actually strikes the rotor). Tilted
wheels are very difficult to find, and level wheels are even rarer.
Almost every wheel is semi-tilted, and on such wheels, every computer
except ours has a dramatically reduced edge. Specifically that is
because 94% of wheels are too tilted to be considered level, but too
level to be considered tilted. In most cases, the resulting accuracy for
simplistic computers is no better than random.
LEFT: The black dots represent where the ball loses momentum and falls from
the ball track for each type of wheel (this is just where the ball loses
momentum and falls, NOT where it actually strikes the rotor). Tilted
wheels are very difficult to find, and level wheels are even rarer.
Almost every wheel is semi-tilted, and on such wheels, every computer
except ours has a dramatically reduced edge. Specifically that is
because 94% of wheels are too tilted to be considered level, but too
level to be considered tilted. In most cases, the resulting accuracy for
simplistic computers is no better than random.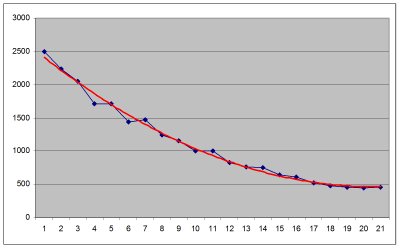
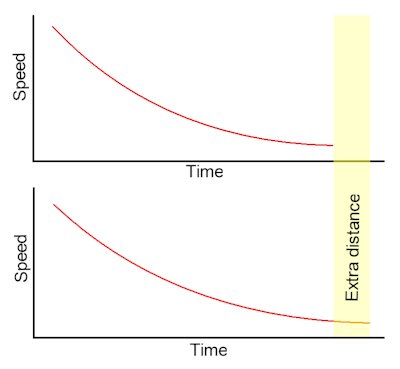 LEFT: In both of these charts, the ball is released at exactly the same
speed. The difference in air pressure and therefore the ball
deceleration rate is only marginal between each chart. However, even
very small deceleration rates make a large difference to the overall
distance traveled by the ball.
LEFT: In both of these charts, the ball is released at exactly the same
speed. The difference in air pressure and therefore the ball
deceleration rate is only marginal between each chart. However, even
very small deceleration rates make a large difference to the overall
distance traveled by the ball.