Scatter is one of the most critical yet misunderstood parts of roulette computer and visual ballistic methods. Simplistically, it is whatever the ball does after it falls from the ball track.
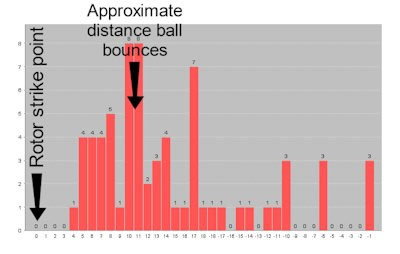
For example, with a simplistic computer algorithm (same as visual ballistics), the player simply collects data consisting of the reference number and winning number in the form of “A,B” as is explained in previous sections. The player hopes to chart this data and see areas in the chart with higher bars in a particular area. An example of this is shown left. Every roulette computer and visual ballistic method uses a chart exactly like this. But most roulette computers do NOT have it built in. For example, my roulette computers enable you to enter the winning number via a hidden cable, then at any time you can view this and other data charts on the screen. But with most other roulette computers, the player needs to manually write down this data on paper, and manually create such a chart. As you can imagine, this is far from an optimal or covert procedure.
A simple chart such as above tells us that most of the time the ball lands 10 or so pockets from the point the ball hits the rotor. But to be accurate, in a situation with a roulette computer or visual ballistics, we directly compare the reference number (A) to the actual winning number (B), and specifically the distance between them.
The Limitations of the Traditional Scatter Chart
First of all, if the roulette computer is incapable of adjusting for ball deceleration rate changes, the accuracy at which it predicts which number will be under the dominant diamond when the ball falls will diminish. This already renders the scatter chart to be useless. But there is also the following problem: The simplistic chart does NOT take into account rotor speed. It incorrectly assumes that the ball will bounce roughly the same distance no matter what the rotor speed is. This is a devastatingly incorrect assumption for many wheels – especially where the pocket separators are low and the ball bounces around a reasonable distance before stopping.
For example, consider two different spins where each time, the ball hit the same diamond, fell, then bounced along before coming to rest. On the first spin, the rotor speed at the time of the ball falling is 4000ms per revolution. On the second spin, the rotor speed is 3000ms. So the second spin has a slightly faster rotor speed. With the difference in rotor speed, will the ball bounce the same distance? . . . NO, but this is what every roulette computer (except my Uber and Hybrid versions) incorrectly assume. The fact is with this almost in perceivable rotor speed variation, the ball may bounce 9 pockets with a 4000ms rotor, and 24 pockets with a 3000ms rotor. This is an enormous difference. So if we merely assume the ball will bounce the same distance regardless of rotor speed, even if we perfectly predict exactly where the ball will hit the rotor (which most computers don’t because of ball deceleration rate changes), your predictions will most certainly have nowhere near maximum possible accuracy.
One particular seller falsely claimed his devices automatically deals with the variation of ball bounce with different rotor speeds. But when confronted with knowledge that his claim was false, he claimed the player only needed to estimate rotor speeds, manually write down the rotor speeds for each spin, then create different scatter charts for each speed range. Then to know where to bet, once the player received the prediction, they would then need to refer back to their charts, determine the optimal offset value for the estimated rotor speed range, then place bets. This is is far from an automated process he initially claimed. Nevertheless, the process is virtually impossible at home, and certainly not possible in a real casino environment. Additionally, such an approach barely holds weight even in theory as much more detailed analysis is required because the relationship between rotor speed and ball bounce is not always linear.
How My Computers Adjust for Different Ball Behavior on Different Rotor Speeds
As a general rule, a faster rotor speed means the ball will bounce further from the rotor strike point. But there is a lot more to it than this. A different rotor speed will affect how erratic the ball will bounce. And on most rotors, specific rotor speeds will produce the least scatter and most predictable ball bounce. For example, on a 3000-3900ms rotor, the ball may bounce very unpredictably. But if the rotor speed is 4000-5000ms, the ball may bounce very predictably. But then if the rotor is slower than 5000ms, you may find the ball bounce is again far less predictable. This rotor speed that produces the most predictable ball bounce is called the “sweet speed”.
A further problem is specific speeds will cause the actual formation of peaks to appear completely differently. For example, over a specific rotor speed threshold, the ball scatter may change from 2 peaks that are 10 pockets apart, to 3 pockets 5 pockets apart.
My Uber and Hybrid computers are the only roulette computers that incorporate accurate solutions to these problems. My devices have the following capabilities:
* Saves and presents the data that enables the player to easily identify and restrict specific rotor speeds that give the most accurate predictions.
* Models the relationship between rotor speed and how far the ball will bounce from the rotor strike point.
* Utilizes two effective solution to the non-linear relationship between rotor speed and ball scatter.
A particular roulette wheel designer I’ve communicated with calls this phenomena, or “variable”, the coefficient of restitution. But the reality is the variables are often too complex to be expressed as a linear relationship. This is because as explained above. different rotor speeds will create a different appearance of scatter. For example, if you used the traditional scatter chart for two sets of 100 spins, but with each set having a significantly different rotor speed, you may find one chart has a single peak (high area of bars), and the other has two peaks that have far weaker definition. My Uber and Hybrid roulette computers address this issue. In particularly the Hybrid precisely defines the relationship between rotor speed and ball scatter.
Other Variables Affecting Ball Scatter
There’s a lot more to ball scatter than just adjusting for different rotor speeds. Below are some of the other variables and how my computers deal with them:
Ball trajectory
The angle at which the ball hits the rotor has an enormous impact on how far the ball will bounce. For example, if the ball is deflected straight down, the ball’s travel distance will not vary much regardless of rotor speed. But as explained in the section about ball deceleration rate changes, the ball’s deceleration rate must be learned dynamically, or it is impossible for the computer to accurately “lock onto” which ever-changing ball speed ranges result in the ball hitting specific diamonds with specific deflection angles. In other words, if the computer does not accurately adjust for ball deceleration rate changes, it will be unable to produce accurate data for analysis, and ultimately unable to model and predict where the ball will bounce based on rotor speed variations. My roulette computers are the only ones available anywhere that do what is required.
Ball fall speed
the faster the ball falls, the further it will bounce. The ball does NOT fall at the same speed on every spin. The fall speed is largely influenced by where it falls. By being able to target where the ball will fall, with consideration to changing conditions such as ball deceleration, my computers can target only spins where the ball falls from the ball track with low momentum. Although ball fall speed is a factor, the relationship between detected ball speed and average trajectory is far more relevant.
My roulette computers are the ones available anywhere that account for all variables affecting scatter including rotor speed, ball trajectory and ball fall speed. In fact every other roulette computer does not even take one of these variables into account. This means the difference between absolutely no accuracy, and very high accuracy.
